Teste de emprego. Devo ser remunerado ou não?

Quando existe mais de duas grandezas envolvidas a regra de três é denominada composta. A grandeza cuja valor é procurado pode ser diretamente ou inversamente proporcional as outras e vice -versa.

Para resolver usamos o mesmo método já estudado anteriormente para resolver a regra de três simples: o das proporções e da redução à unidade.

Quanto mais máquinas trabalhando, menos dias para produzir a quantidade
planejada. (Fonte : Wikimedia)

Método das proporções - exemplo:

Em 6 dias de trabalho produzem-se 720 uniformes escolares fazendo funcionar 16 máquinas de costura. Em quantos dias se podem aprontar 2160 uniformes escolares fazendo funcionar somente 12 máquinas?

Resolução:

Temos a seguinte disposição prática:

6 dias  720 unif.  16 máq.

 x         2160      12

Fixando a 3° grandeza (n° de máquinas), vemos que a 1° grandeza (n° de dias) e a 2° (n° de uniformes) são diretamente proporcionais, pois, duplicando o valor de uma delas duplicará o valor da outra. Fixando agora a 2° grandeza, observamos que a 1° e a 3° são inversamente proporcionais, pois, ao duplicar o número de máquinas o número de dias empregado para fabricar os uniformes irá diminuir.

Assim sendo a disposição passará a ser:

ou, invertendo os valores correspondentes da 3° grandeza:

Observação: a propriedade que caracteriza a existência de uma grandeza diretamente proporcional a várias outras - os valores que exprimem sua medida são diretamente proporcional aos produtos dos valores correspondentes das outras:

Construindo a respectiva proporção temos:

Logo, serão necessários 24 dias para se aprontarem 21600 uniformes utilizando 12 máquinas.

Método da redução à unidade. (utilizando o mesmo exemplo).

Se com 16 máquinas se fazem 720 uniformes em 6 dias com 1 máquina se fazem 720 uniformes em 6 x 16 dias.

E com 1 máquina se faz 1 uniforme em 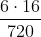   dias.

Logo, 12 máquinas farão 1 uniforme em 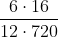   dias,

e 12 máquinas farão 2160 uniformes em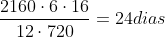 

Observação: Na resolução da regra de três composta utilizando qualquer um dos métodos, pode-se utilizar a seguinte regra prática:

• Colocam-se dispostas de forma prática as diversas grandezas presentes no problema;
• Invertem-se as posições dos dois valores correspondentes das diversas grandezas que são inversamente proporcionais ( 16 e 12 foram os valores trocados no exemplo utilizado), em relação à grandeza cuja variação da incógnita X se procura.
• O valor de X é dado pela fração que tem para numerador os seguintes valores: o oposto de X (6 no exemplo) e os pertencentes à mesma linha de X ( 2160 e 12 no exemplo) e para denominador o produto dos valores pertencentes à outra linha ( 720 e 12 no exemplo).

Vamos praticar? 

Exercício resolvido utilizando a regra de três composta:

- Os engenheiros calcularam que, para construir uma ponte, uma equipe de 200 operários levaria 150 dias trabalhando 6 horas por dia. Mas houve uma mudança de plano para conter os custos e agilizar a obra. Dessa forma, o número de trabalhadores caiu para 180 e a carga horária subiu para 10 horas. Nessas condições, em quantos dias a ponte vai ficar pronta?

Resolvendo:

Para resolver este exercício utilizando a regra de três composta, precisamos analisar primeiro quais são as grandezas envolvidas:

- Número de operários

- Carga horária de trabalho

- Total de dias para a conclusão da obra

Para montar a regra de três composta é preciso comparar cada grandeza duas a duas, identificando se elas são diretamente ou inversamente proporcionais.

- Comparando número de operários e o total de dias:

         Grandezas
Operários   Total de dias
   200               150
   180                 𝓧

Com 200 operários, a ponte será concluída em 150 dias. Com menos trabalhadores, o trabalho demoraria mais. Ou seja, essas duas grandezas são inversamente proporcionais.

- Comparando a carga diária e o total de dias.

           Grandezas
Carga Diária   Total de dias
       6                    150
      10                      𝓧

Trabalhando 6 horas, a ponte ficaria pronta em 150 dias. Trabalhando 10 horas, a ponte ficaria pronta em menos dias. Ou seja, essas duas grandezas também são inversamente proporcionais.

Agora podemos montar a proporção. Mas atenção: Como a grandeza "Total de dias" é inversamente proporcional às grandezas "Operários" e "Carga diária", é preciso invertêlas na proporção. Veja como fica:

Resposta do Exercício: A ponte ficará pronta em 100 dias com 180 funcionários trabalhando 10 horas por dia.

Editoração e pesquisa:

Luciane Gasparin